Logistics - Motor Bench Tester - Magnetizer -Tension system - Form Rolling Machine - Winding machine - Balanceing machie
バランシングマシン - 転造盤 - 巻線機 - テンション装置 - 着磁機 - モータ特性試験機 - ロジスティックス

戻   る

フーリエ変換

  計測データ処理の基本としてサンブリング定理、フーリエ変換、デジタルフィルタはさけて通れません。 制御ではラプラス変換、Z変換が基本です。ここでは実際の計測、モータの制御を取り上げ実用の範囲で説明します。
　

.i  フーリエ級数

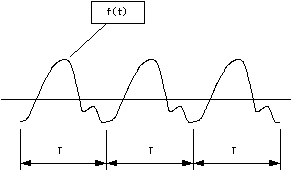
周期関数f(t)は三角関数の級数で表すことが出来る。この三角関数の級数をフーリエ級数と云います。

周期関数とはTを周期とし繰返す関数で、f(t)=f(t+nT) (n=0,±1,±1,±1,‥)となります。

 

 

 

 

 

 


図 1　周期関数

 

フーリエ級数を数式で表すと

 

 
 
 
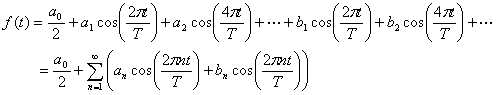 ここで、a,bをフーリエ係数と言います。


フーリエ係数は次のように求めます。
 
 
  .ii 複素フーリエ級数
オイラーの公式を使い指数関数でフーリエ級数を表します。
オイラーの公式は



 

  
 

 

  
  
 




 
 
ここで、eit   ,cost,sintのテーラ展開は
 



 

  
 

 

  
  
 




 
  



 

  
 

 

  
  
 




 
 
 
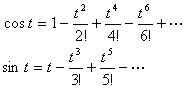となりますから、オイラーの公式が求められます。
 cost,sintはオイラーの公式をもちいて表すと
 



 

  
 

 

  
  
 




 
 
 
 
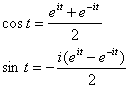 これを用いて



 

  
 

 

  
  
 




 
 
 
 
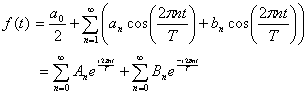 と指数を用いて表せます。フーリエ係数も指数を用いて表すと
 



 

  
 

 

  
  
 




 
 
 
 
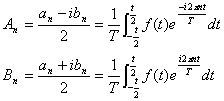 ここで指数部の符号はnを−まで拡張すれば



 

  
 

 

  
  
 




 
 



 

  
 

 

  
  
 




 
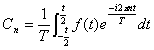        (nは−まで拡張)
 となり、シンプルな表現となり、これを複素フーリエ級数と云います。
 

 .iii                   フーリエ積分 

 <後日に続く　FFT 自己相関　クロススペクトル　セプストラム　を説明>