はじめにバタワースフィルタの振幅特性を示します。
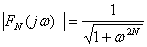
| 戻 る |
| 計測データ処理の基本としてサンブリング定理、フーリエ変換、デジタルフィルタはさけて通れません。 制御ではラプラス変換、Z変換が基本です。ここでは実際の計測、モータの制御を取り上げ実用の範囲で説明します。 また、システムの全体の動作を制御するシーケンスプログラムはPLCラダー、C,VC,VBの使用を前提として説明します。 |
アナログフィルタにはチェビシェフ、楕円、バタワースなどとよばれる色々な特性があります。ここでは代表的なバタワース特性のローバスフィルタを例にデジタルフィルタの設計を説明します。
はじめにバタワースフィルタの振幅特性を示します。
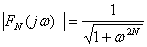
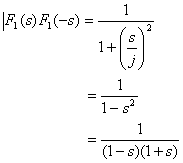 よって、極は s=±1 となります。
ここで、伝達関数の安定の条件から、極は平面左側に無ければいけませんから 1/(s+1) が安定な一次のバタワースフィルタの伝達関数となります。 次にN=
2のバタワースフィルタの伝達関数を求めて見ます。
一次と同様に振幅を表すしきにsを代入すると
よって、極は s=±1 となります。
ここで、伝達関数の安定の条件から、極は平面左側に無ければいけませんから 1/(s+1) が安定な一次のバタワースフィルタの伝達関数となります。 次にN=
2のバタワースフィルタの伝達関数を求めて見ます。
一次と同様に振幅を表すしきにsを代入すると
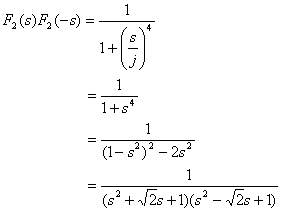 ここで、S平面の虚軸より左に極がある因数を選べば安定項は
ここで、S平面の虚軸より左に極がある因数を選べば安定項は 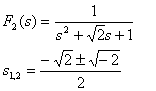 となります。
となります。 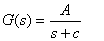
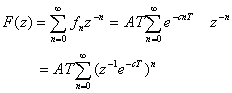 となりますから、これの級数和を求めれば
となりますから、これの級数和を求めれば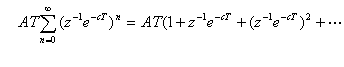 よって
よってが得られます。
.B 双一次変換
z変換は s-平面の嘘軸より左の領域をz-平面の半径
1の円の内側に写像します。デジタルフィルタのラプラス変換はアナログフィルタのスペクトルを±方向に2π/Tの距離で繰り返します。従ってZ
変換ではこの繰り返しもz-平面に写像されてしまいす。サンブル間隔によっては繰り返(折り返し)されるスペクトルがお互い緩衝し希望の性能が実現出来ない場合があります。そこでz-変換する前にs-平面全体を-π/T
~+π/T の範囲に写像してしまうことを考えます。
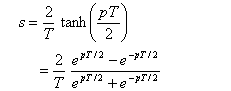
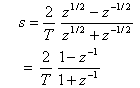
 となります。
となります。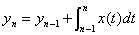
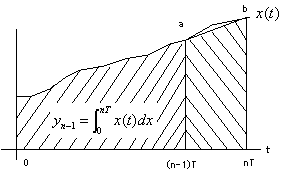 ここで上式の右辺の第2項の積分を台形近似します。
ここで上式の右辺の第2項の積分を台形近似します。 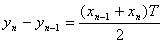 両辺をラプラス変換をして
両辺をラプラス変換をして
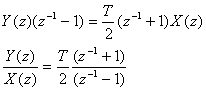
を得ます。これは先に挙げたsの式の逆数となっています。なぜなら、積分演算のラプラス変換は1/sだからです。これを改めてsとすれば両式は一致し双一次変換が求められたことになります。以上の結果を用いてデジタルのバタワースフィルタを計算します。バタワースフィルタの伝達関数は
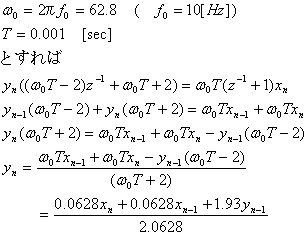
上式をエクセルなどで計算しフィルタ動作の確認をして下さい。
|
ご意見
ご質問 (AUXデザイン 担当 善如寺までご遠慮なくどうぞ)
(ご質問が特許出願準備中の件、または守秘に関する項目の場合はご回答出来かねます
|