Logistics - Motor Bench Tester - Magnetizer -Tension system - Form Rolling Machine - Winding machine - Balanceing machie
バランシングマシン - 転造盤 - 巻線機 - テンション装置 - 着磁機 - モータ特性試験機 - ロジスティックス

戻   る

計測と制御について
計測データ処理の基本としてサンブリング定理、フーリエ変換、デジタルフィルタはさけて通れません。 制御ではラプラス変換、Z変換が基本です。ここでは実際の計測、モータの制御を取り上げ実用的範囲で説明します。 また、システムの全体の動作を制御するシーケンスプログラムはPLCラダー、C,VC,VBの使用を前提に説明します。


2          Z変換

.i  サンプル値系列のz変換

サンプル値系列をｘ(nT)とし

             

 

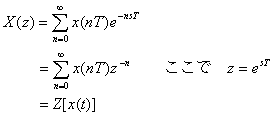
上式はサンプル系列x(nT)のz変換を表し、n=0,1,2,・・・と与えられる無限和で表されます。

ここでesTはラプラス変換の無駄時間に相当しますから、これはxをTだけ遅らさせるとも考えられます。

従ってz-1は１サンブル遅らさせた信号と解釈できます。

.ii 離散値信号のラブラス変換からZ変換

サンブリング周期をTとしてアナログ信号x(t)をサンブリングしたときのf*(t)は

となります。そこでで両辺をラプラス変換します。

 

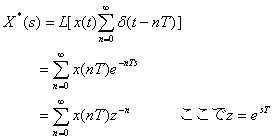
ここでZとsの関係を調べますと、s平面の虚軸より左が全てz平面の半径1の円の内側に写像

され、s平面の右側はz-平面の半径1の円の外側に写像される事になります。
ここでs=σ+iωとおき、

 

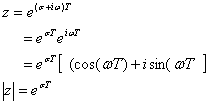
よって、σ>0 で|z|>1となりますから上の関係が証明されました。

伝達関数の安定条件はs-平面左に極があることですからZ-平面では半径1の円の内側に極が存在すれば

安定と言云うことになります。

安定の条件について

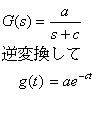
となります。ここでG(s)が−の極をもてばg(t)は無限時間後0となります。もしG(s)の極がブラスに

存在すればg(t)は時間とともに成長し発散します。従って系は不安定となります。