![]()
| 戻 る |
|
計測データ処理の基本としてサンブリング定理、フーリエ変換、デジタルフィルタはさけて通れません。
制御ではラプラス変換、Z変換は基本です。ここでは実際の計測、モータの制御を取り上げ実用的範囲で説明します。
また、システムの全体の動作を制御するシーケンスプログラムは、PLCラダー、C,VC,VBの使用を前提として説明します。 |
はじめに、δ関数(単位インパルス関数)について説明します。
δ関数は次のように定義されます。
|
|
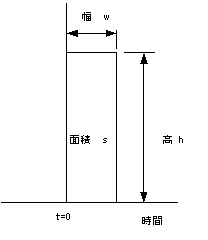
図 1 方形パルス
図1で、δ関数はw ×h =1
の方形パルスの
幅と高さの関係をw=1/hとしてw→0とした関数と見なせます。
ここで、計測データをx(t)として次式が成立します。
![]()
w →0であるから積分の平均の定理を用いて
![]()
となりますから、δ(t) によりx(t)のt=0時点の値が切り出された訳けです。
図 2 方形パルスによるサンプル
図2で、面積s=1の方形パルスを用いてx(t)を
サンプルする直感的な説明をします。
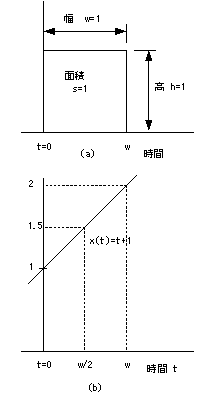
図2の(a)で方形パルスをf(t)と置き
f(t)×x(t)を考えます。時間t=0からt=wの区間の
f(t)×x(t)の面積を求めます。
f(t)はこの区間で1ですから図2の(b)図で
は時間軸とx(t)で囲まれた面積となります。
s=h (x(0)+x(1))w/2
=1×(1+ 2)×1/2
=1.5
=x(0.5)
次に、方形するパルスの幅
s=h (x(0)+x(0.5)) w/2
=2×(1+ 1.5)×0.5/2
=1.25
=x(0.25)
ここで h×wは常に1ですから面積は
s=(x(0)+x(w))/2
=x(w/2)
となります。
ここでwを限りなく0に近づければs=x(0)となりt=0の
x(t)の値が切り出せました。
この結果は先の説明と一致します。
δ関数を用いてx(t)のτ時点の値の切り出しは次式で表せます。
![]()
δ(t)をτだけ遅らせx(t)に掛けて積分します。τをt=0からの遅れ時間とすればx(t)のt=τの時の値が切り出せる事になります。
このことからδ関数を一定間隔で並べたインパルス関数列を考え、計測データx(t)との積を−∞が+∞まで積分することを考えます。インパルス列は
![]()
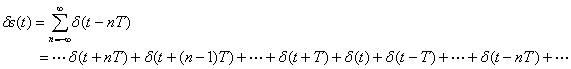
このδ関数をt=Tの間隔で並べたインパルス列を用いれば計測信号x(t)を時間間隔Tのとびとびの値として切り出せます。ここでTをサンブリング周期とし、計測信号x(t)(連続時間信号)のサンブリングされた飛び飛びの信号をx*(t)(離散信号という)とすればサンプリングは次式で表されます。
![]()
計測信号がt<0でx(t)=0であれば
![]()
上式はtがnTと一致した瞬間だけx(t)の値を切りだすことを表してします。ですからx*(t)は連続信号のx(t)のT間隔毎の値の飛び飛びの信号並びとなります。
δs(t)をフーリエ級数に展開することを考えます。
![]()
と表せます。フーリエ係数αnは次式となります。
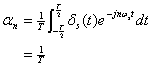
αnは全てのnで1/Tとなります。従って
![]()
これを用いて計測信号のサンプル列x*(t)を再び表せば
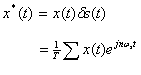
両辺をラプラス変換すれば
![]() X(s)は連続信号x(t)のラプラス変換
X(s)は連続信号x(t)のラプラス変換
s=jωとおけば
![]()
となります。
よってサンプル信号のスペクトルは時間連続信号x(t)のスペクトルをωsとし、このスペクトルを-∞から+∞に配置した形となります 。
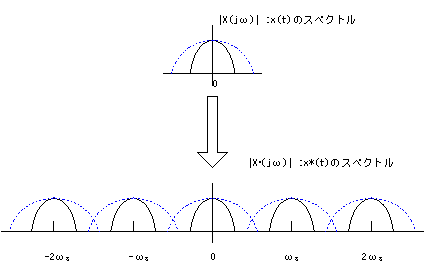 |
図3 時間連続信号x(t)と離散信号x(t)*のスペクトルの比較
図3に時間連続信号のスペクトル|X(jω)|と離散信号のスペクトル|X*(jω)|の比較を表します。図から時間連続信号のスペクトルがωs/2の範囲にあればサンブリングされた後のスペクトルの配置に緩衝が現れないことが分かります。従って時間連続の信号x(t)はインパルス列δs(t)の繰り返し周波数fs=1/Tの1/2以下であればサンブリング後もx(t)の情報が保存されることを示しています。すなわちサンブル信号を必要な周波数帯だけを弁別出来る Low-Pass Filterを用いれば元々の時間連続信号x(t)の再生が出来ると言うことです。
この時間連続信号とサンブル周波数の関係をサンブリング定理と言います。